Global Illumination / Indirect Lighting

  • A broad term that refers to any algorithm or technique that simulates how light bounces around a scene, not just directly from light sources but also after interactions with surfaces.

  • It encompasses both direct lighting  (light coming straight from a source) and indirect lighting  (light that has bounced one or more times).

Terms

Irradiance

  • Irradiance (scalar) :

    • At a surface point, the integral of incoming radiance over the hemisphere (units: W/m²).

    • Often the quantity of interest for diffuse shading.

  • Irradiance field :

    • An Irradiance Field is the continuous phenomenon.

    • A function that maps spatial position (and sometimes orientation) to irradiance.

    • In papers this term can mean the true continuous field, or a specific continuous representation (e.g., a voxel grid, analytic basis, or neural field).

  • Irradiance probes :

    • An Irradiance Probe is a discrete measurement of that phenomenon.

    • A set of sampled measurements placed at discrete spatial locations.

    • Each probe stores an irradiance representation (examples: spherical-harmonic coefficients, a small cubemap, or directional coefficients).

    • During rendering the scene samples/interpolates between probes to approximate the irradiance at arbitrary points.

Techniques

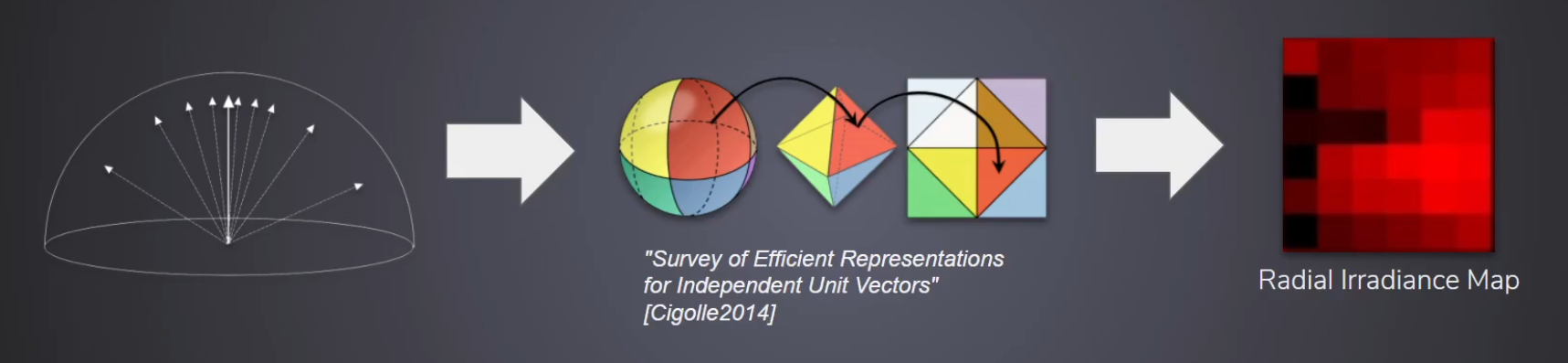
Parameterizations / sampling layouts for the sphere

Octahedral Maps

  • A bijective mapping (with a fold) that encodes a unit 3D direction n = (x,y,z)  into 2D texture coordinates u,v ∈ [0,1] .

  • Designed to pack the sphere into a single square texture with less angular distortion than latitude–longitude and usually fewer wasted texels than cube maps.

  • Commonly used to store normals, unit vectors (reflection vectors, tangent-space directions), or per-direction scalar/vector fields (e.g., an environment map sampled per texel).

Cube Maps

  • Filament Importance Sampling for the IBL .

  • Precomputing $L_{DFG}$ :

    • The term $L_{DFG}$ is only dependent on $n.v$. Below, the normal is arbitrarily set to $n = [0, 0, 1]$ and $v$ is chosen to satisfy $n.v$. The vector $h_i$ is the $D_{GGX}(\alpha)$ important direction sample $i$. 

    float GDFG(float NoV, float NoL, float a) {
    float a2 = a * a;
    float GGXL = NoV * sqrt((-NoL * a2 + NoL) * NoL + a2);
    float GGXV = NoL * sqrt((-NoV * a2 + NoV) * NoV + a2);
    return (2 * NoL) / (GGXV + GGXL);
}

float2 DFG(float NoV, float a) {
    float3 V;
    V.x = sqrt(1.0f - NoV*NoV);
    V.y = 0.0f;
    V.z = NoV;

    float2 r = 0.0f;
    for (uint i = 0; i < sampleCount; i++) {
        float2 Xi = hammersley(i, sampleCount);
        float3 H = importanceSampleGGX(Xi, a, N);
        float3 L = 2.0f * dot(V, H) * H - V;

        float VoH = saturate(dot(V, H));
        float NoL = saturate(L.z);
        float NoH = saturate(H.z);

        if (NoL > 0.0f) {
            float G = GDFG(NoV, NoL, a);
            float Gv = G * VoH / NoH;
            float Fc = pow(1 - VoH, 5.0f);
            r.x += Gv * (1 - Fc);
            r.y += Gv * Fc;
        }
    }
    return r * (1.0f / sampleCount);
}

  • Filament Engine coordinates system :

    • .

    • To simplify the rendering of reflections, IBL cubemaps are stored mirrored on the X axis. This is the default behaviour of the cmgen  tool. This means that an IBL cubemap used as environment background needs to be mirrored again at runtime. An easy way to achieve this for skyboxes is to use textured back faces. Filament does this by default.

    • To convert equirectangular environment maps to horizontal/vertical cross cubemaps we position the +Z face in the center of the source rectilinear environment map.

    • When specifying a skybox or an IBL in Filament, the specified cubemap is oriented such that its -Z face points towards the +Z axis of the world (this is because filament assumes mirrored cubemaps). However, because environments and skyboxes are expected to be pre-mirrored, their -Z (back) face points towards the world's -Z axis as expected (and the camera looks toward that direction by default).

Directional Data (Represent or approximate functions on the sphere (bases or parametric lobes))

When an SH/SG/wavelet can “replace” a cubemap/oct map — and when it cannot

  • Replace (acceptable / typical):

    • Low-frequency lighting (diffuse irradiance): SH (low-order) is commonly used instead of sampling a full cubemap at runtime because SH compactly encodes low-frequency content and allows analytic convolution with Lambertian cosine. That avoids per-pixel cubemap lookups for diffuse IBL.

    • Compact specular approximation: Representing an environment by a small number of SG lobes can replace a cubemap for fast approximate glossy shading or importance sampling when the environment is lobe-like.

    • Compression / streaming: Wavelets (or hierarchical transforms) can replace a naive cubemap storage by providing a compressed, multiresolution representation that is progressively refinable.

  • Cannot fully replace (or will be lossy / expensive to use):

    • Detailed, high-frequency reflections (sharp mirror-like): Full-resolution cubemap/oct textures or prefiltered mipmap chains (PMREM) are the usual approach. SH needs very high band count (many coefficients) to represent sharp features, and SG requires many lobes to approximate complex high-frequency structure — both become expensive or inaccurate.

    • Arbitrary sampling and filtering: A texture parameterization (cubemap/oct) is a direct sampling representation and is straightforward to sample, filter (with caveats) and prefilter with hardware. Basis expansions require projection and reconstruction steps before sampling in the standard pipeline.

Haar Wavelets

  • A family of localized, multiresolution basis functions (Haar is the simplest wavelet) that represent signals with coarse-to-fine detail. Haar wavelets are piecewise-constant, have compact support, and provide spatial locality and hierarchical decomposition.

  • Typical form (1D/2D idea):  scaling functions and wavelet functions that split signal into averages + differences at successive scales. On the sphere one can build analogous spherical wavelet bases (e.g., via hierarchical partitioning of the sphere).

  • Properties:  spatially localized, multi-resolution (supports progressive refinement), good at representing localized/high-frequency features and discontinuities, many coefficients are zero or small for sparse signals, not globally smooth (Haar is discontinuous). Wavelet transforms can be fast (O(n)). Rotation is awkward for bases tied to a fixed partitioning.

  • Common graphics uses:  compression and multi-resolution representation of environment maps or textures, adaptive shading, fast hierarchical importance sampling / level-of-detail, GPU-friendly encodings, and sparse approximations of signals with local sharp features.

  • Trade-offs:  better for localized/high-frequency structure and compression; Haar specifically is low-order (blocky) unless higher-order wavelets are used; rotation and analytic convolution are not generally simple in the wavelet domain without additional structure.

Spherical Gaussians (SG)

  • What it is (short):  parametric, localized “lobe” functions on the sphere that approximate a single-peaked angular distribution (an axis-aligned Gaussian-like lobe).

  • Typical form (common form):  $G(\omega;\mu,\kappa)=\exp\big(\kappa(\mu\cdot\omega-1)\big)$, where $\mu$ is the lobe axis and $\kappa$ (or similar) controls concentration (larger $\kappa$ = narrower lobe). (Different papers use slightly different normalization/scales.)

  • Properties:  strongly localized, easily rotated by changing $\mu$, analytic approximations exist for products and convolutions with some BRDF lobes (useful approximations), compact parametric representation (axis + sharpness), cheap evaluation of a single lobe. Not an orthogonal basis. Multiple SGs can be summed to approximate complex lobes.

  • Common graphics uses:  representing specular lobes and glossy reflections, analytic or semi-analytic shading and convolution approximations, importance sampling, fitting environment lighting with a sum of lobes for real-time shading. SGs are also used in prefiltered environment maps where single-lobe behavior is important.

  • Trade-offs:  simple and efficient for localized lobes; approximating arbitrary functions requires many SGs; not linear-orthonormal (so projection/coefficients don’t have the same algebraic niceties as SH).

Spherical Harmonics (SH)

  • An Efficient Representation for Irradiance Environment Maps - Ramamoorthi & Hanrahan - Siggraph 2001 .

  • Frequency Space Environment Map Rendering - Ramamoorthi & Hanrahan- Siggraph 2002 .

    • "Spherical harmonic reflection map (SHRM)".

  • Lighting and Material of Halo 3 - Siggraph 2008 .

  • Lighting and Material of Halo 3 - Siggraph 2008 .

    • Bungie pioneered baked SH lighting in a shipped game with Halo 3 (Xbox 360, 2007). Halo 3’s engine precomputed “light probe” textures: each texel stored multiple SH coefficients (the slides cite 9–16 floats per texel) representing the incoming diffuse light at that point. These SH lightmaps were then sampled in shaders, so that static geometry received baked global illumination, and dynamic models could be lit by dot-producting their SH transfer vectors against the light-probe SH. (Siggraph 2008 “Lighting and Materials of Halo 3” notes SH lightmaps as a natural extension of lightmaps.

  • Filament - Spherical Harmonics .

    • C++ implementation to compute a non-normalized SH basis: 

    static inline size_t SHindex(ssize_t m, size_t l) {
    return l * (l + 1) + m;
}

void computeShBasis(
        double* const SHb,
        size_t numBands,
        const vec3& s)
{
    // handle m=0 separately, since it produces only one coefficient
    double Pml_2 = 0;
    double Pml_1 = 1;
    SHb[0] =  Pml_1;
    for (ssize_t l = 1; l < numBands; l++) {
        double Pml = ((2 * l - 1) * Pml_1 * s.z - (l - 1) * Pml_2) / l;
        Pml_2 = Pml_1;
        Pml_1 = Pml;
        SHb[SHindex(0, l)] = Pml;
    }
    double Pmm = 1;
    for (ssize_t m = 1; m < numBands ; m++) {
        Pmm = (1 - 2 * m) * Pmm;
        double Pml_2 = Pmm;
        double Pml_1 = (2 * m + 1)*Pmm*s.z;
        // l == m
        SHb[SHindex(-m, m)] = Pml_2;
        SHb[SHindex( m, m)] = Pml_2;
        if (m + 1 < numBands) {
            // l == m+1
            SHb[SHindex(-m, m + 1)] = Pml_1;
            SHb[SHindex( m, m + 1)] = Pml_1;
            for (ssize_t l = m + 2; l < numBands; l++) {
                double Pml = ((2 * l - 1) * Pml_1 * s.z - (l + m - 1) * Pml_2)
                        / (l - m);
                Pml_2 = Pml_1;
                Pml_1 = Pml;
                SHb[SHindex(-m, l)] = Pml;
                SHb[SHindex( m, l)] = Pml;
            }
        }
    }
    double Cm = s.x;
    double Sm = s.y;
    for (ssize_t m = 1; m <= numBands ; m++) {
        for (ssize_t l = m; l < numBands; l++) {
            SHb[SHindex(-m, l)] *= Sm;
            SHb[SHindex( m, l)] *= Cm;
        }
        double Cm1 = Cm * s.x - Sm * s.y;
        double Sm1 = Sm * s.x + Cm * s.y;
        Cm = Cm1;
        Sm = Sm1;
    }
}

    • C++ code to compute $\hat{C}_l$: 

    static double factorial(size_t n, size_t d = 1);

// < cos(theta) > SH coefficients pre-multiplied by 1 / K(0,l)
double computeTruncatedCosSh(size_t l) {
    if (l == 0) {
        return M_PI;
    } else if (l == 1) {
        return 2 * M_PI / 3;
    } else if (l & 1) {
        return 0;
    }
    const size_t l_2 = l / 2;
    double A0 = ((l_2 & 1) ? 1.0 : -1.0) / ((l + 2) * (l - 1));
    double A1 = factorial(l, l_2) / (factorial(l_2) * (1 << l));
    return 2 * M_PI * A0 * A1;
}

// returns n! / d!
double factorial(size_t n, size_t d ) {
   d = std::max(size_t(1), d);
   n = std::max(size_t(1), n);
   double r = 1.0;
   if (n == d) {
       // intentionally left blank
   } else if (n > d) {
       for ( ; n>d ; n--) {
           r *= n;
       }
   } else {
       for ( ; d>n ; d--) {
           r *= d;
       }
       r = 1.0 / r;
   }
   return r;
}

  • Basis functions $Y_{\ell}^m(\theta,\phi)$ indexed by degree $\ell\ge 0$ and order $-\ell\le m\le\ell$. A function $f(\omega)$ on the sphere is expanded as $f(\omega)=\sum_{\ell=0}^{L}\sum_{m=-\ell}^{\ell} c_{\ell m} Y_{\ell}^m(\omega)$.

  • Are an orthonormal basis for functions on the sphere. In real-time lighting they are used to compactly represent low-frequency angular functions (environment illumination, visibility, convolution kernels).

  • Irradiance probes commonly store SH coefficients so the renderer can approximate diffuse lighting quickly.

  • Why is it useful for Irradiance / Probes :

    • Compression : low-frequency lighting (diffuse environment lighting, soft shadows) is well-approximated by a small number of SH bands (e.g. 9 coefficients).

    • Linear projection : you can project an environment (cubemap, sampling) onto SH. Once you have certain coefficients​, you store those in a probe instead of storing a full cubemap.

    • Fast evaluation : to evaluate the approximated radiance or irradiance at some direction $\omega$, evaluate the SH basis at $\omega$ and form the dot product with coefficients: $f(\omega)=\sum a_{l}^{m}Y_{l}^{m}(\omega)$. That dot product is inexpensive for small L.

    • Convolution property (why diffuse works well) : for Lambertian reflection you need the cosine-weighted integral of incoming radiance. The cosine kernel is low-frequency and its SH representation has non-zero weight only on low bands. Convolving $L_i$​ with the cosine kernel reduces to scaling SH bands by precomputed factors. Practically, this means you can compute irradiance from the projected SH coefficients cheaply without re-sampling the entire environment at render time.

  • Spherical Harmonics Demo .

    • A demonstration of spherical harmonics used to construct the surface of the earth at increasing angular resolution.

  • Spherical Harmonics Demo - Earth Magnetic Field .

  • Spherical Harmonics Visualization .

    • We describe the possible fundamental vibrations on a sphere in three dimensions by counting, mirroring and rotating nodal lines.

  • Spherical Harmonics Demo .

    • Idk, wtf.

  • Spherical Harmonics in Quantum Mechanics .

    • The video is cool.

    • The idea is to take this 1D visualization for the energy states of the electron:

    •  

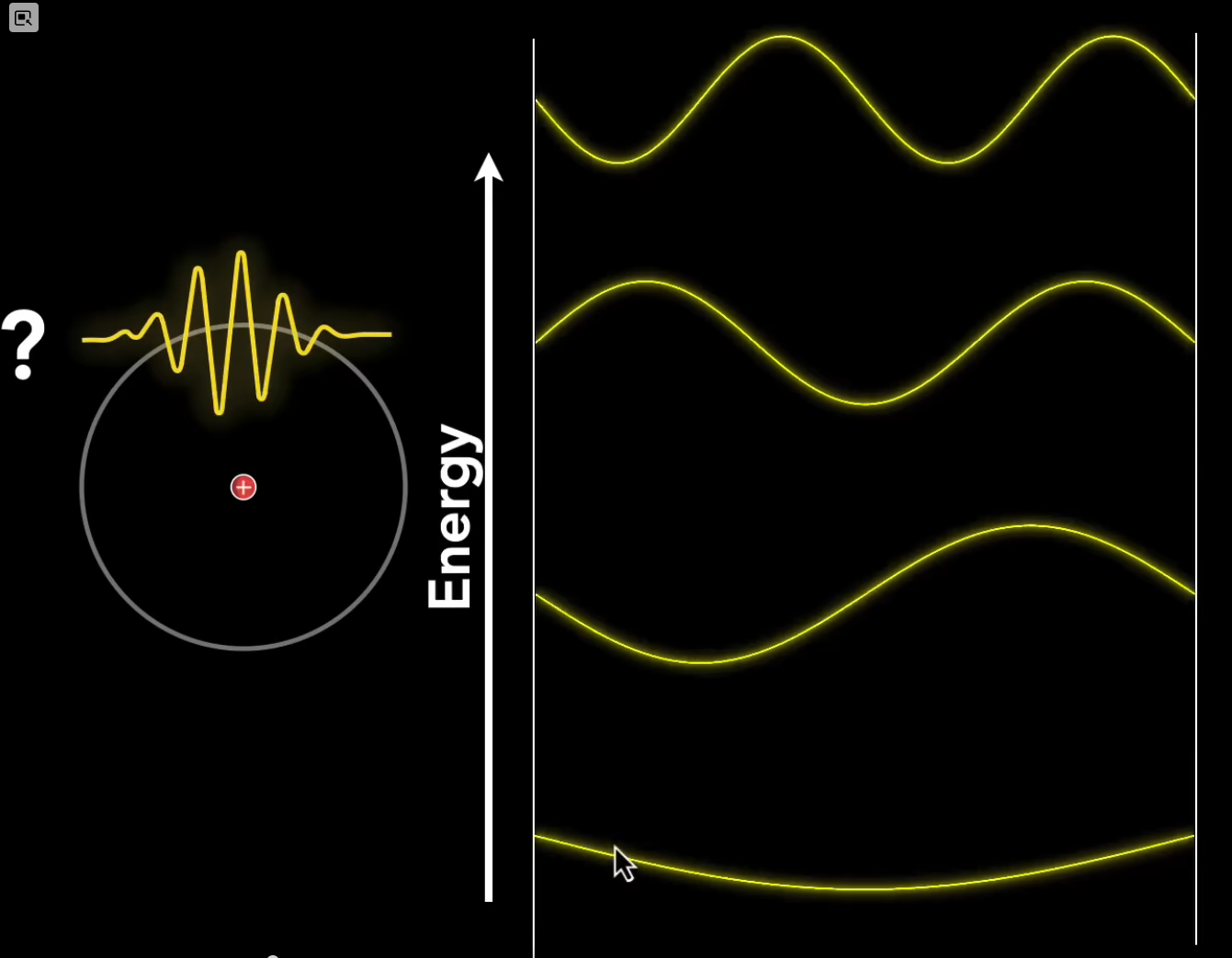
    • And arrive at this 3D visualization:

    • .

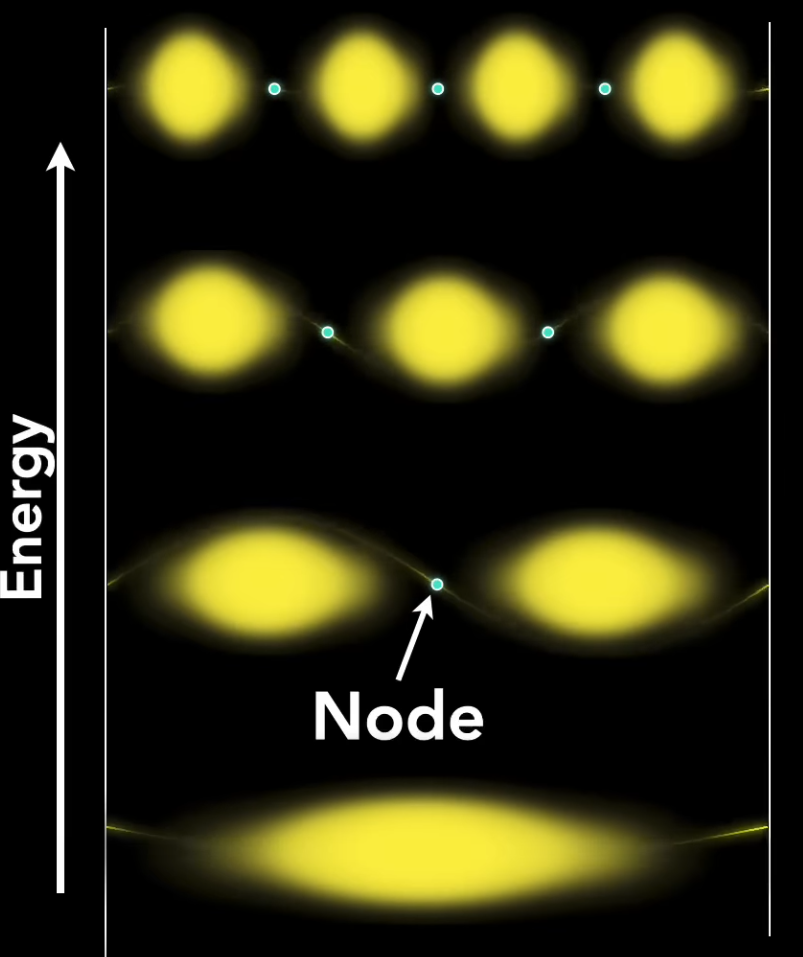
    • All the visual characteristics of the visualization come from the ways in which the nodes can be represented.

    • Apparently nodes can be radial or angular. The angular representations appear when considering that the node can be a plane.

    • It is these nodes represented as a plane that make the shapes more interesting.

  • The "overlap" I mentioned is not about spatial overlap. It's about mathematical independence.

  • Spherical harmonics are precisely the spherical analogue of the Fourier transform.

  • Fourier Series (for a function on a circle):  Any function on a 1D circle (like a sound wave over time) can be broken down into a sum of simple, orthogonal basis functions: sines and cosines of different frequencies ( sin(nθ) , cos(nθ) ).

    • The low-frequency sines/cosines capture the broad, smooth shape.

    • The high-frequency ones capture the sharp details and edges.

  • Spherical Harmonics (for a function on a sphere):  Any function on a 2D sphere (like an environment map) can be broken down into a sum of simple, orthogonal basis functions: the spherical harmonics ( Y_lm(θ, φ) ).

    • The low- l  (low-frequency) SHs capture the broad, smooth lighting (the average color, the dominant light direction).

    • The high- l  (high-frequency) SHs capture the sharp details and edges (sharp reflections, tiny light sources).

  • We are not projecting a 3D scene onto a sphere.

    • This is called environment map capture (e.g., taking a 360° photo). That gives us a function f(θ, φ)  that is defined on the surface of a sphere.

  • The Spherical Harmonic transform is the next step. We are taking that already-spherical function f(θ, φ)  and projecting it onto the spherical harmonic basis functions.

  • The word "projection" here is used in the linear algebra sense, just like projecting a vector onto a set of basis axes.

  • Imagine your environment map f(ω)  is a vector in a giant, infinite-dimensional space.

  • The spherical harmonics Ylm(ω)  form a complete set of orthonormal basis vectors for that space.

  • Projecting f  onto a specific basis vector Ylm  is how we find the coefficient clm  for that function. The formula for this projection is the inner product:   c_lm = ∫ f(ω) * Y_lm(ω) dω .

  • This is identical to how in 3D space, you find the x -component of a vector V  by projecting it onto the unitX basis vector: V_x = V • unitX .

  • "Orthonormalization"  means we have ensured two things for our basis functions Y_lm :

    • Orthogonal:   ∫ Y_lm(ω) * Y_l'm'(ω) dω = 0  if (l, m) ≠ (l', m')  (they are independent).

    • Normalized:   ∫ Y_lm(ω) * Y_lm(ω) dω = 1  (each one has a "unit length").

  • This orthonormality is what makes the math so clean and the coefficients independent.

  • In Quantum Mechanics, the spherical harmonics Y_lm  are famous because they are the angular solutions to the Laplace equation in spherical coordinates.

  • This describes the probability distribution of an electron around a hydrogen atom (its orbital). The shapes of the s, p, d, f orbitals are visualizations of the Y_lm  functions!

    • Y00  is the s-orbital (spherical).

    • Y1m  are the three p-orbitals (dumbbell shaped along x, y, z).

    • Y2m  are the five d-orbitals (cloverleaf shapes).

  • In Computer Graphics:  We are using the exact same mathematical functions to describe the distribution of light energy around a point. The "orbital" is now the "irradiance environment."

  • The key difference is one of interpretation:

  • In Quantum Mechanics, you're solving for a wavefunction.

  • In Computer Graphics, you're using the SH basis to compactly represent a function (light) defined on a sphere.

  • The process for computer graphics :

    • For a render engineer, the process is this:

    1. Capture/Define:  Start with an environment map f(ω) . This is your function on the sphere.

    2. Project (Precompute/Integrate):  For each SH basis function Y_lm  you care about (e.g., the first 9), compute the coefficient c_lm  by integrating the product f(ω) * Y_lm(ω)  over the entire sphere. This is the "transformation" into the SH frequency space.   c_lm = ∫ f(ω) * Y_lm(ω) dω

    3. Reconstruct (Runtime):  To get the approximate value of the environment at any direction ω , you evaluate the sum:   f(ω) ≈ Σ c_lm * Y_lm(ω)  for l=0...N-1 .

  • The reason this is a "convolution" is that the rendering equation often includes a cosine term ( n • ω ). The magic is that projecting this cosine lobe into SH space results in analytic attenuation factors ( A_l ) that you can just multiply by your c_lm  coefficients before  the reconstruction step. This turns a complex integral into a simple dot product of two SH vectors (lighting coefficients and attenuated coefficients).

  • So, you were right on all counts. It is a Fourier-style transform. It is a projection onto an orthonormal basis. And it uses the same elegant math as quantum physics to solve a seemingly unrelated problem in computer graphics with breathtaking efficiency.

  • Application :