-
Graphics Rendering Introduction .
-
Nice, with plenty of animations.
-
Concepts
-
Homogeneous coordinates (4D) :
-
Representation that lets projection be expressed as a linear 4×4 matrix and supports perspective divide.
-
-
Affine Transformations :
-
Preserves:
-
Straight lines (no curves introduced)
-
Parallelism (parallel lines remain parallel, though distances can change)
-
Ratios along a line (midpoints stay midpoints)
-
An affine transformation has the last row fixed to
[0,0,0,1]. -
Affine examples :
-
Translation
-
Rotation
-
Uniform/non-uniform scaling
-
Shearing
-
Any combination of the above
-
-
Non-affine examples :
-
Perspective projection (parallel lines may converge)
-
Non-linear warps
-
-
-
Note :
-
'Matrix' and 'Transform Matrix' are the same thing in this context.
-
Everything is separated between Spaces, Matrices, or operations.
-
-
 .
.
-
 .
.
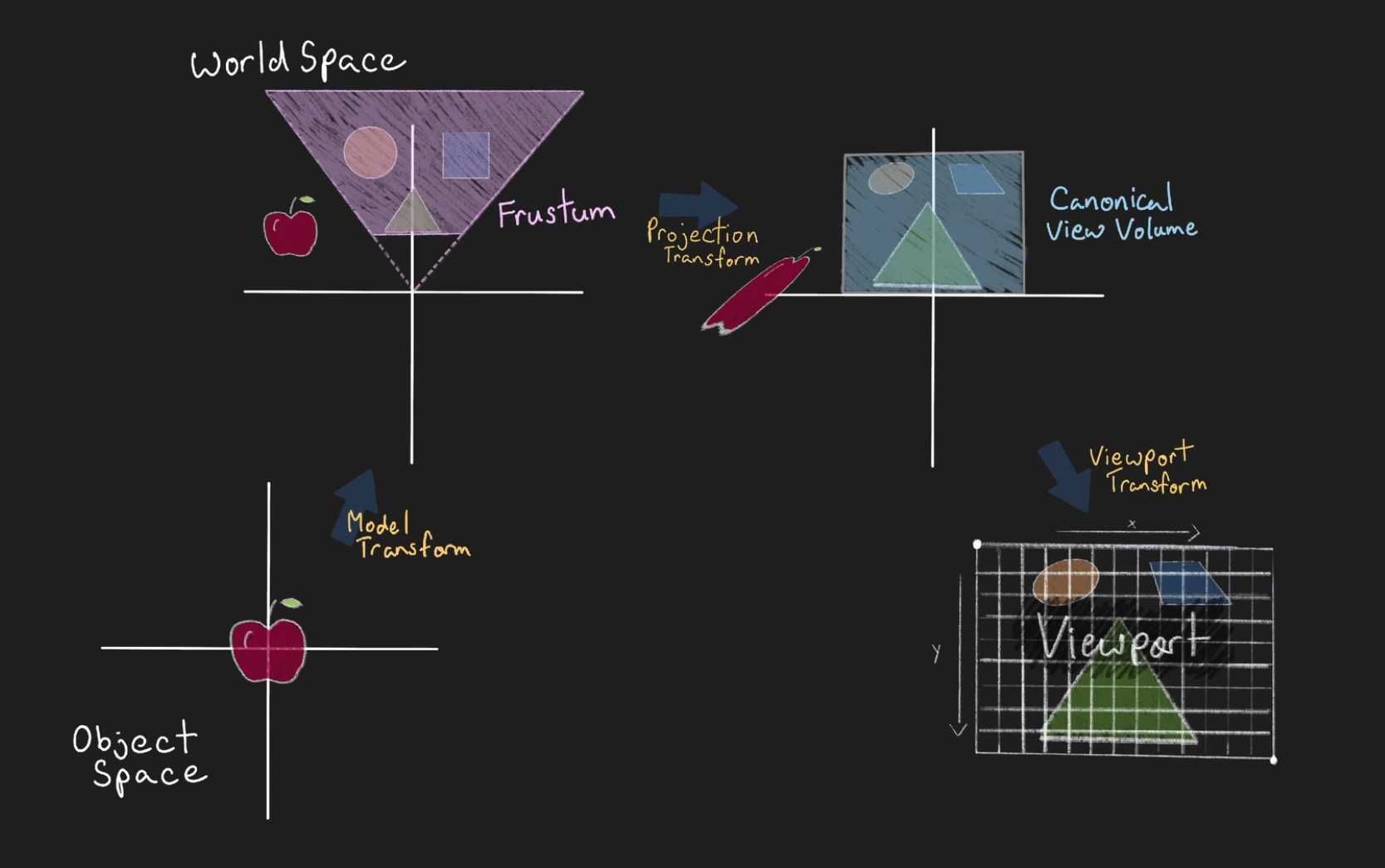
Model / Object / Local Space
-
A coordinate space where a single mesh or object’s vertices are defined relative to the object’s own origin.
-
Vertices are usually created and manipulated in object space before any scene-level transforms are applied.
Model / Object / Local Matrix
-
Transforms Model / Object / Local Space into World Space .
-
It's an affine transformation.
-
Applies the object’s translation, rotation, scale (and optionally shear).
World Space
-
A scene-level coordinate system in which multiple objects are placed and arranged.
-
World space is the reference for lighting, physics, and global placement.
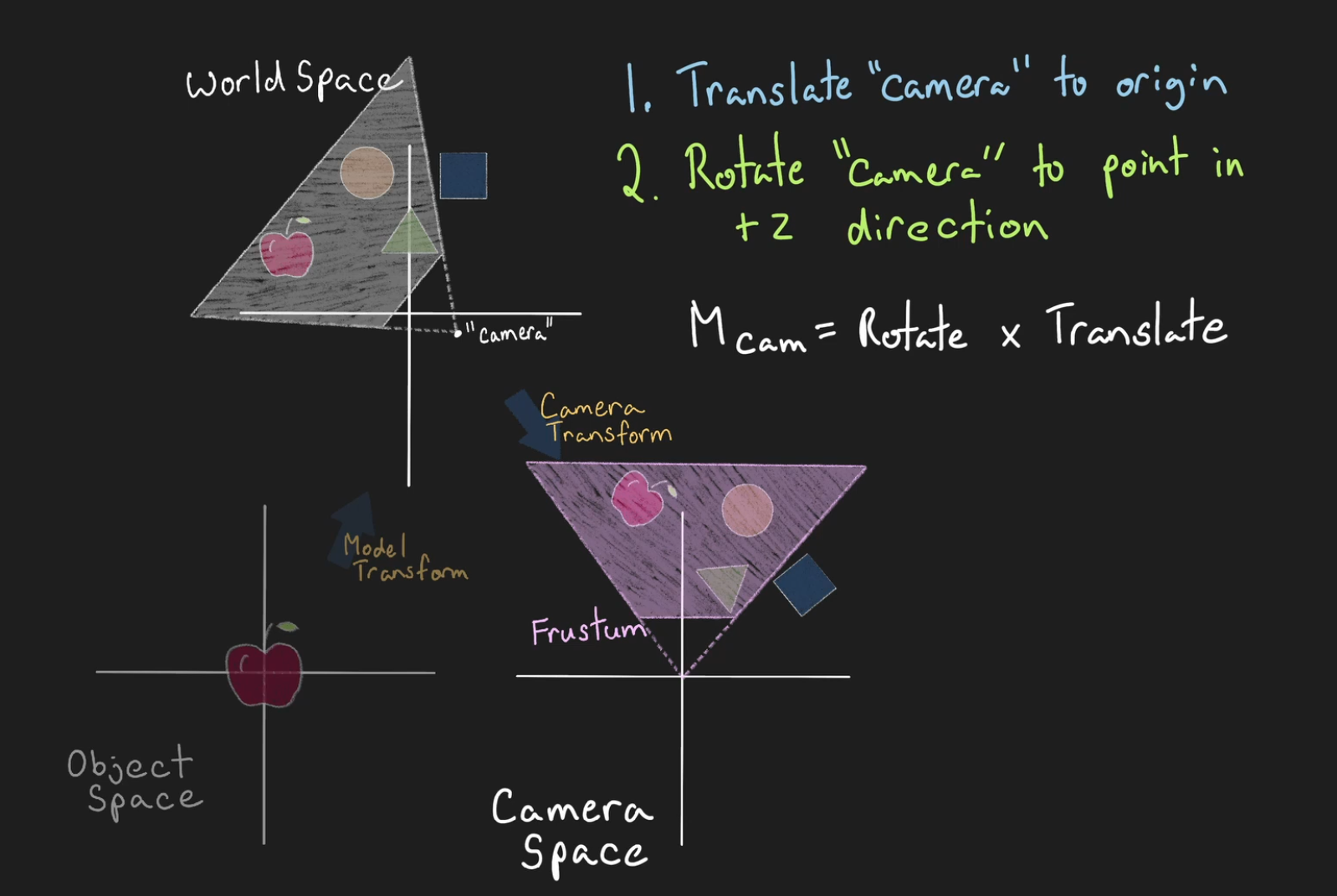
Camera / View / Eye Matrix
-
Transforms World Space into Camera / View / Eye Space .
-
It's an affine transformation.
-
The inverse of a camera’s world transform.
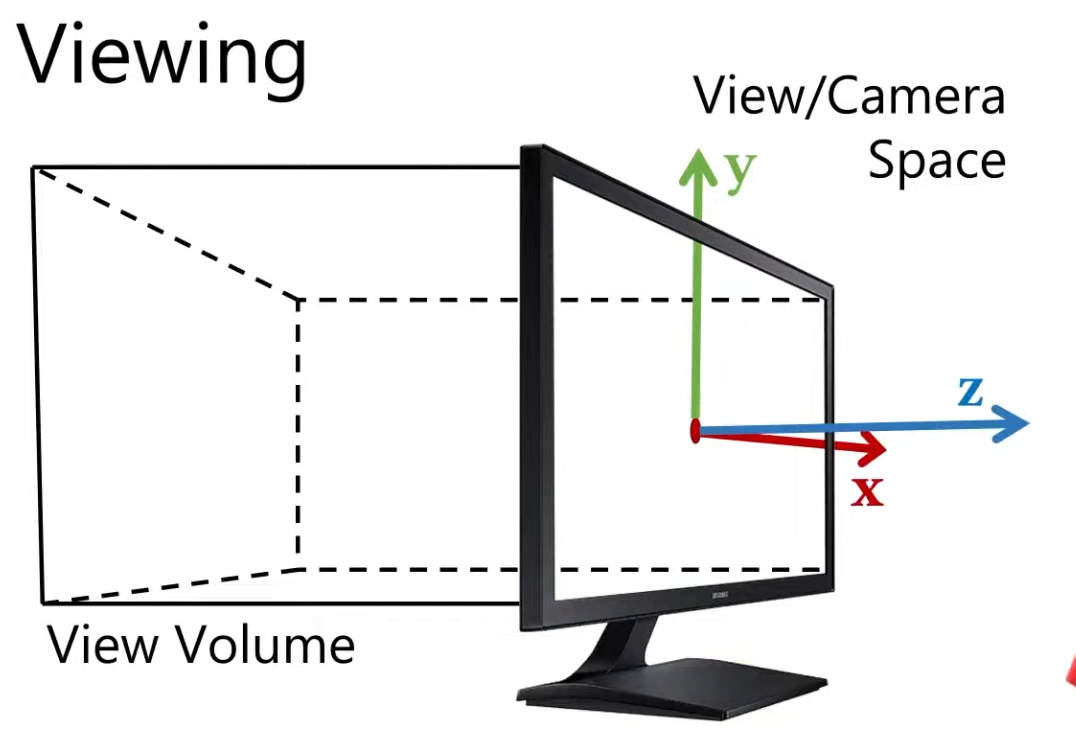
Camera / View / Eye Space
-
A coordinate system where the camera is at the origin and looks down a canonical axis (commonly −Z or +Z depending on convention).
-
Vertices are expressed relative to the camera: positions are what the camera “sees.”
-
 .
.
Projection Matrix / Classical-Z / Reversed-Z
-
Transforms all vertices from the Camera / View / Eye Space into Clip Space .
-
The GPU later Clips to the frustum.
-
The projection matrix doesn’t “ignore” vertices outside the frustum; it still transforms them.
-
-
Is defined by the View Frustum parameters.
-
It's not an affine transformation, as they rely on a divide by
w(the Perspective Divide ). -
Reverse Z (and why it's so awesome) - Tom Hulton-Harrop .
-
The best article on the topic.
-
-
Vulkan Projection Matrix - Vincent Parizet .
-
The explanation seems correct, but I'm quite sure his formulas use row_major, instead of column major.
-
-
-
I'm not sure I should trust this source.
-
perspective_infinite_z_vkwas incorrect.
-
-
Definitions :
-
vertical_fov-
Should be provided in radians.
-
-
aspect_ratio-
Should be the quotient
width / height.
-
-
What matters
-
Handedness :
-
It matters.
-
-
Which axis is vertical in NDC :
-
It matters.
-
-
Depth range :
-
It matters.
-
-
Y Up vs Z Up :
-
It doesn't matter.
-
Classical-Z / Reversed-Z
-
Also check #Precision .
Vulkan
-
Flipping the Y axis is required because Vulkan's Y axis in clip space points down.
-
Other options :
-
Flipping y in the shader.
-
Setting a negative height for the viewport.
-
With reverse z it’s possible to just flip the order of the near and far arguments when using the regular projection matrix.
-
For whatever reason I prefer the above approach but please do what’s best for you and be aware of these other approaches out in the wild.
-
-
-
Classical-Z :
-
Finite :
-
Right Handed :
-
Direct result:
@(require_results) camera_perspective_vulkan_classical_z :: proc "contextless" (vertical_fov, aspect, near, far: f32) -> (m: Mat4) #no_bounds_check { /* Right-handed (Camera forward -Z). Clip Space: left-handed, y-down, with Z (depth) extending from 0.0 (close) to 1.0 (far). */ focal_length := 1.0 / math.tan(0.5 * vertical_fov) nmf := near - far m[0, 0] = focal_length / aspect m[1, 1] = -focal_length m[2, 2] = far / nmf m[3, 2] = -1 m[2, 3] = near * far / nmf return }-
Manually: Take the OpenGL projection matrix, remap the depth from 0 to 1, and then additionally flip the Y axis.
mat4 perspective_vulkan_rh(const float fovy, const float aspect, const float n, const float f) { constexpr mat4 vulkan_clip {1.0f, 0.0f, 0.0f, 0.0f, 0.0f, -1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.5f, 0.0f, 0.0f, 0.0f, 0.5f, 1.0f}; return mat_mul(perspective_opengl_rh(fovy, aspect, n, f), vulkan_clip); // The correct multiplication is vulkan_clip * perspective_opengl_rh (column-vector math) } -
-
-
Infinite :
-
Right Handed :
@(require_results) camera_perspective_vulkan_infinite :: proc "contextless" (vertical_fov, aspect, near: f32) -> (m: Mat4) #no_bounds_check { /* Right-handed (Camera forward -Z). Clip Space: left-handed, y-down, with Z (depth) extending from 1.0 (close) to 0.0 (far). */ focal_length := 1.0 / math.tan(0.5 * vertical_fov) A :: -1.0 B := near m[0, 0] = focal_length / aspect m[1, 1] = -focal_length m[2, 2] = A m[3, 2] = -1 m[2, 3] = B return }
-
-
-
Reversed-Z :
-
Clear depth to 0 (not 1 as usual).
-
Set depth test to greater (not less as usual).
-
Ensure you’re using a floating point depth buffer (e.g.
GL_DEPTH_COMPONENT32F,DXGI_FORMAT_D32_FLOAT_S8X24_UINT,MTLPixelFormat.depth32Floatetc.) -
Finite :
-
Right Handed :
@(require_results) camera_perspective_vulkan_reversed_z :: proc "contextless" (vertical_fov, aspect, near, far: f32) -> (m: Mat4) #no_bounds_check { /* Right-handed (Camera forward -Z). Clip Space: left-handed, y-down, with Z (depth) extending from 1.0 (close) to 0.0 (far). */ /* This procedure assumes near < far. If near > far, the depth will be inverted, and far away geometry will be drawn first; which is incorrect. */ return camera_perspective_vulkan_classical_z(vertical_fov, aspect, far, near) }-
Vulkan Reversed-Z Finite - Vincent Parizet .
-
I tested his version and it doesn't work for me.
-
If I transpose his version, it works fine.
-
His matrices are probably row-major, not column-major.
-
-
-
-
Infinite :
-
Right Handed :
@(require_results) camera_perspective_vulkan_reversed_z_infinite :: proc "contextless" (vertical_fov, aspect, near: f32) -> (m: Mat4) #no_bounds_check { /* Right-handed (Camera forward -Z). Clip Space: left-handed, y-down, with Z (depth) extending from 1.0 (close) to 0.0 (far). */ focal_length := 1.0 / math.tan(0.5 * vertical_fov) A :: 0 B := near m[0, 0] = focal_length / aspect m[1, 1] = -focal_length m[2, 2] = A m[3, 2] = -1 m[2, 3] = B return }-
Vulkan Reversed-Z Infinite - Vincent Parizet .
-
I tested his version and it doesn't work for me.
-
If I transpose his version, it becomes exactly equal to the implementation above, and it works fine.
-
His matrices are probably row-major, not column-major.
-
-
-
-
-
Orthographic :
-
Right Handed :
/// Clip-space: left-handed and y-down with Z (depth) clip extending from 0.0 (close) to 1.0 (far). #[inline] pub fn orthographic_vk(left: f32, right: f32, bottom: f32, top: f32, near: f32, far: f32) -> Mat4 { let rml = right - left; let rpl = right + left; let tmb = top - bottom; let tpb = top + bottom; let fmn = far - near; Mat4::new( Vec4::new(2.0 / rml, 0.0, 0.0, 0.0), Vec4::new(0.0, -2.0 / tmb, 0.0, 0.0), Vec4::new(0.0, 0.0, -1.0 / fmn, 0.0), Vec4::new(-(rpl / rml), -(tpb / tmb), -(near / fmn), 1.0), ) }
-
DirectX / Metal
-
Uses 0 for the near plane and 1 for the far plane.
-
Classical-Z :
-
Finite :
-
Right Handed :
// The resulting depth values mapped from 0 to 1. mat4 perspective_direct3d_rh(const float fovy, const float aspect, const float n, const float f) { const float e = 1.0f / std::tan(fovy * 0.5f); return {e / aspect, 0.0f, 0.0f, 0.0f, 0.0f, e, 0.0f, 0.0f, 0.0f, 0.0f, f / (n - f), -1.0f, 0.0f, 0.0f, (f * n) / (n - f), 0.0f}; }/// Meant to be used with WebGPU or DirectX. /// Clip-space: left-handed and y-up with Z (depth) clip extending from 0.0 (close) to 1.0 (far). #[inline] pub fn perspective_wgpu_dx(vertical_fov: f32, aspect_ratio: f32, z_near: f32, z_far: f32) -> Mat4 { let t = (vertical_fov / 2.0).tan(); let sy = 1.0 / t; let sx = sy / aspect_ratio; let nmf = z_near - z_far; Mat4::new( Vec4::new(sx, 0.0, 0.0, 0.0), Vec4::new(0.0, sy, 0.0, 0.0), Vec4::new(0.0, 0.0, z_far / nmf, -1.0), Vec4::new(0.0, 0.0, z_near * z_far / nmf, 0.0), ) } -
Left Handed :
// The resulting depth values mapped from 0 to 1. mat4 perspective_direct3d_lh(const float fovy, const float aspect, const float n, const float f) { const float e = 1.0f / std::tan(fovy * 0.5f); return {e / aspect, 0.0f, 0.0f, 0.0f, 0.0f, e, 0.0f, 0.0f, 0.0f, 0.0f, f / (f - n), 1.0f, 0.0f, 0.0f, (f * n) / (n - f), 0.0f}; }
-
-
Infinite :
-
Right Handed :
/// Meant to be used with WebGPU, or DirectX. /// Clip-space: left-handed and y-up with Z (depth) clip extending from 0.0 (close) to 1.0 (far). #[inline] pub fn perspective_infinite_z_wgpu_dx(vertical_fov: f32, aspect_ratio: f32, z_near: f32) -> Mat4 { let t = (vertical_fov / 2.0).tan(); let sy = 1.0 / t; let sx = sy / aspect_ratio; Mat4::new( Vec4::new(sx, 0.0, 0.0, 0.0), Vec4::new(0.0, sy, 0.0, 0.0), Vec4::new(0.0, 0.0, -1.0, -1.0), Vec4::new(0.0, 0.0, -z_near, 0.0), ) }
-
-
-
Reverse-Z :
-
Clear depth to 0 (not 1 as usual).
-
Set depth test to greater (not less as usual).
-
Ensure you’re using a floating point depth buffer (e.g.
GL_DEPTH_COMPONENT32F,DXGI_FORMAT_D32_FLOAT_S8X24_UINT,MTLPixelFormat.depth32Floatetc.) -
Finite :
-
Right Handed :
/// Meant to be used with WebGPU, OpenGL, or DirectX. /// Clip-space: left-handed and y-up with Z (depth) clip extending from 0.0 (close) to 1.0 (far). /// Note: In order for this to work properly with OpenGL, you'll need to use the `gl_arb_clip_control` extension /// and set the z clip from 0.0 to 1.0 rather than the default -1.0 to 1.0. #[inline] pub fn perspective_reversed_z_wgpu_dx_gl( vertical_fov: f32, aspect_ratio: f32, z_near: f32, z_far: f32, ) -> Mat4 { let t = (vertical_fov / 2.0).tan(); let sy = 1.0 / t; let sx = sy / aspect_ratio; let nmf = z_near - z_far; Mat4::new( Vec4::new(sx, 0.0, 0.0, 0.0), Vec4::new(0.0, sy, 0.0, 0.0), Vec4::new(0.0, 0.0, -z_far / nmf - 1.0, -1.0), Vec4::new(0.0, 0.0, -z_near * z_far / nmf, 0.0), ) }
-
-
Infinite :
-
Right Handed :
/// Meant to be used with WebGPU, OpenGL, or DirectX. /// Clip-space: left-handed and y-up with Z (depth) clip extending from 0.0 (close) to 1.0 (far). /// Note: In order for this to work properly with OpenGL, you'll need to use the `gl_arb_clip_control` extension /// and set the z clip from 0.0 to 1.0 rather than the default -1.0 to 1.0. #[inline] pub fn perspective_reversed_infinite_z_wgpu_dx_gl( vertical_fov: f32, aspect_ratio: f32, z_near: f32, ) -> Mat4 { let t = (vertical_fov / 2.0).tan(); let sy = 1.0 / t; let sx = sy / aspect_ratio; Mat4::new( Vec4::new(sx, 0.0, 0.0, 0.0), Vec4::new(0.0, sy, 0.0, 0.0), Vec4::new(0.0, 0.0, 0.0, -1.0), Vec4::new(0.0, 0.0, z_near, 0.0), ) }
-
-
-
Orthographic :
-
Right Handed :
/// Clip-space: left-handed and y-up with Z (depth) clip extending from 0.0 (close) to 1.0 (far). #[inline] pub fn orthographic_wgpu_dx( left: f32, right: f32, bottom: f32, top: f32, near: f32, far: f32, ) -> Mat4 { let rml = right - left; let rpl = right + left; let tmb = top - bottom; let tpb = top + bottom; let fmn = far - near; Mat4::new( Vec4::new(2.0 / rml, 0.0, 0.0, 0.0), Vec4::new(0.0, 2.0 / tmb, 0.0, 0.0), Vec4::new(0.0, 0.0, -1.0 / fmn, 0.0), Vec4::new(-(rpl / rml), -(tpb / tmb), -(near / fmn), 1.0), ) }
-
Legacy OpenGL
-
Uses −1 for the near and 1 for the far. This is the worst for floating point precision.
-
Classical-Z :
-
Finite :
-
Right-handed :
// The resulting depth values mapped from -1 to +1. mat4 perspective_opengl_rh(const float fovy, const float aspect, const float n, const float f) { const float e = 1.0f / std::tan(fovy * 0.5f); return {e / aspect, 0.0f, 0.0f, 0.0f, 0.0f, e, 0.0f, 0.0f, 0.0f, 0.0f, (f + n) / (n - f), -1.0f, 0.0f, 0.0f, (2.0f * f * n) / (n - f), 0.0f}; } -
Left-handed :
// The resulting depth values mapped from -1 to +1. mat4 perspective_opengl_lh(const float fovy, const float aspect, const float n, const float f) { const float e = 1.0f / std::tan(fovy * 0.5f); return {e / aspect, 0.0f, 0.0f, 0.0f, 0.0f, e, 0.0f, 0.0f, 0.0f, 0.0f, (f + n) / (f - n), 1.0f, 0.0f, 0.0f, (2.0f * f * n) / (n - f), 0.0f}; } -
Normalizing Matrix :
// map from -1 to 1 to 0 to 1 mat4 normalize_unit_range(const mat4& perspective_projection) { constexpr mat4 normalize_range {1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.5f, 0.0f, 0.0f, 0.0f, 0.5f, 1.0f}; return mat_mul(perspective_projection, normalize_range); // The correct multiplication is normalize_range * perspective_projection (column-vector math) }
-
-
Infinite :
-
Right-handed :
/// Clip-space: left-handed and y-up with Z (depth) clip extending from -1.0 (close) to 1.0 (far). #[inline] pub fn perspective_infinite_z_gl(vertical_fov: f32, aspect_ratio: f32, z_near: f32) -> Mat4 { let t = (vertical_fov / 2.0).tan(); let sy = 1.0 / t; let sx = sy / aspect_ratio; Mat4::new( Vec4::new(sx, 0.0, 0.0, 0.0), Vec4::new(0.0, sy, 0.0, 0.0), Vec4::new(0.0, 0.0, -1.0, -1.0), Vec4::new(0.0, 0.0, -2.0 * z_near, 0.0), ) }
-
-
-
Reverse-Z :
-
Use the Normalizing Matrix above, and the Reverse-Z Matrix below, to get the final Proj Matrix.
-
We create a standard perspective matrix and update the depth mapping to be from -1 to 1 to 0 to 1 (all the matrix is doing is multiplying by 0.5 then adding 0.5 to achieve this).
const mat4 perspective_projection = perspective_opengl_rh(radians(60.0f), float(width) / float(height), near, far); const mat4 reverse_z_perspective_projection = reverse_z(normalize_unit_range(perspective_projection));-
Steps :
-
Clear depth to 0 (not 1 as usual).
-
Set depth test to greater (not less as usual).
-
Ensure you’re using a floating point depth buffer (e.g.
GL_DEPTH_COMPONENT32F,DXGI_FORMAT_D32_FLOAT_S8X24_UINT,MTLPixelFormat.depth32Floatetc.) -
(in OpenGL) Make sure
glClipControl(GL_LOWER_LEFT, GL_ZERO_TO_ONE);is set so OpenGL knows the depth range will be 0 to 1 and not -1 to 1. -
Extra that I saw somewhere: you'll need to use the
gl_arb_clip_controlextension and set the z clip from 0.0 to 1.0 rather than the default -1.0 to 1.0
-
-
-
Orthographic :
-
Right-handed :
/// Clip-space: left-handed and y-up with Z (depth) clip extending from -1.0 (close) to 1.0 (far). #[inline] pub fn orthographic_gl(left: f32, right: f32, bottom: f32, top: f32, near: f32, far: f32) -> Mat4 { let rml = right - left; let rpl = right + left; let tmb = top - bottom; let tpb = top + bottom; let fmn = far - near; let fpn = far + near; Mat4::new( Vec4::new(2.0 / rml, 0.0, 0.0, 0.0), Vec4::new(0.0, 2.0 / tmb, 0.0, 0.0), Vec4::new(0.0, 0.0, -2.0 / fmn, 0.0), Vec4::new(-(rpl / rml), -(tpb / tmb), -(fpn / fmn), 1.0), ) }
-
Reverse-Z
-
1 for the near plane and 0 for the far plane.
-
 .
.
-
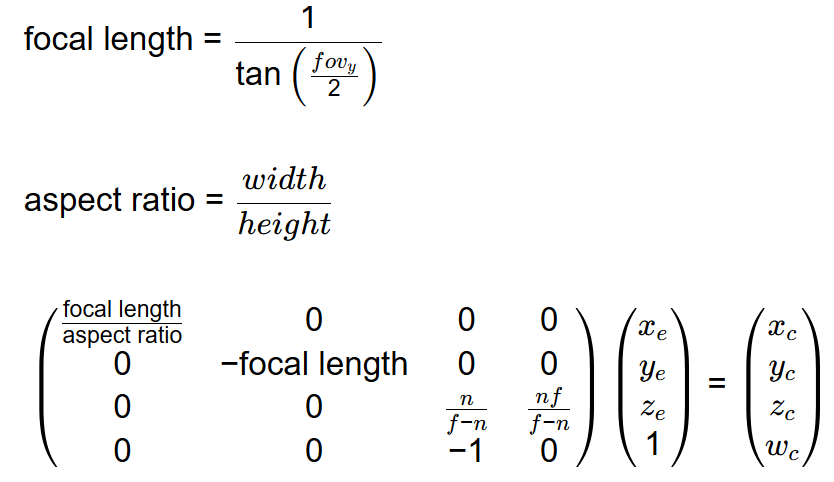 .
.
-
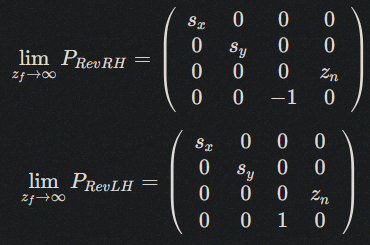 .
.
-
Reverse Z Matrix :
-
We can just swap the
nearandfarparameters when calling the function. -
Or we can create a new matrix that will produce a reverse Z friendly matrix for us.
-
This matrix flips the z/depth value to go from 1 to 0 instead of 0 to 1.
mat4 reverse_z(const mat4& perspective_projection) { constexpr mat4 reverse_z {1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, -1.0f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f}; return mat_mul(perspective_projection, reverse_z); // The correct multiplication is reverse_z * perspective_projection (column-vector math) }-
Note :
-
I tested doing this, but it simply didn't work.
-
-
-
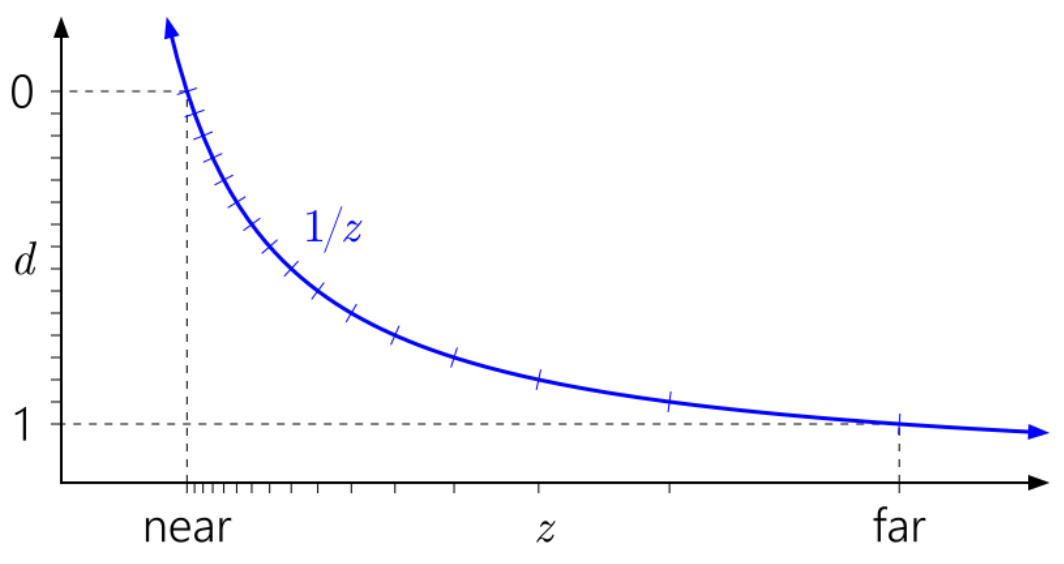
Precision :
-
Results in a better distribution of the floating point values than using −1 and 1 or 0 and 1.
-
There is a truly insane amount of precision near 0 with floating point numbers.
-
Out of the total range between 0.0 and 1.0, only approximately 0.79% of all representable values are between 0.5 and 1.0, with a staggering 99.21% between 0.0 and 0.5.
-
I always knew there was more precision near 0, but I don’t think I’d fully appreciated by quite how much.
-
Example :
-
Non-Reversed-Z:
-
If we choose a generous near clip plane of 1.0 and far clip plane of 100.0, and give an input value of say 5.0 to this equation we get an interesting result. The depth value is 0.808! That means even when we’re using regular z, and we have a value near the clip plane, we already have completely discarded an insane amount of precision because all those values near 0 already can’t be used. If we put in more representative numbers things get even worse. With a near clip plane of 0.01 and a far clip plane of 1000.0, using a view space depth value of 5.0 gives 0.998. That means we only have 33554 unique values left to represent normalized depth between 5.0 and 1000 which isn’t great.
-
-
Reversed-Z:
-
Now for the near clip plane at 1.0 and far clip plane at 100.0 case, with an input value of 5.0, we get approximately 0.192 for the depth value. If we set the near clip plane to 0.01 and the far clip plane to 1000, a view space depth value of 5.0 becomes approximately 0.00199. The amazing thing though is in this case we have 990014121 possible unique depth values, an improvement of 29500x over regular z.
-
Reversing z has the effect of smoothing the precision throughout the range (we leverage the fact so much precision sits between 0.0 and 0.5 by ensuring more values end up there). Without reverse z, the precision is front-loaded to the near clip plane where we don’t need as much precision.
-
The incredible thing about this is we gain all this extra precision and improved fidelity at no cost in performance or memory, which usually never happens in computer science or software engineering
-
-
-
-
Usage in Orthographic Projection :
-
The depth precision gain is negligible. Orthographic mapping is linear in z, so the standard forward mapping already distributes precision uniformly.
-
You should only do it if your renderer globally uses reverse-Z for consistency (e.g. shared depth buffer with perspective passes), otherwise, keep Classical-Z.
-
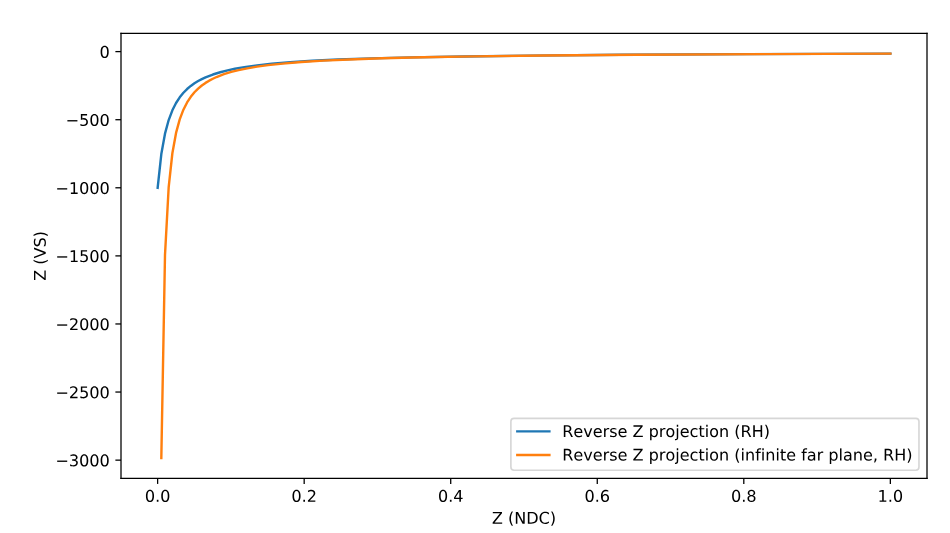
Infinite Perspective
-
Having to set scene-specific values for both the near and far plane can be a pain in the ass. If you want to display large open-world scenes, you will almost always use an absurdly high value for the far plane anyway.
-
With the increased precision of using a Reverse-Z, it is possible to set an infinitely distant far plane.
-
 .
.
-
Usage in Orthographic Projection :
-
Orthographic projections define a finite slab of space. Sending
far → ∞removes the far clipping plane, but all geometry at any z beyondnearwill still map to the same NDC z value (0 or 1 depending on convention). -
Depth test stops discriminating depth beyond the near plane, so almost everything “at infinity” z-fights.
-
It is mathematically valid but useless for depth testing. It can be used only if you never rely on depth ordering—e.g. for skybox or background plane rendering.
-
Nvidia Recommendations
-
Article .
-
The
1/z(Reversed-Z) mapping and the choice of float versus integer depth buffer are a big part of the precision story, but not all of it. Even if you have enough depth precision to represent the scene you're trying to render, it's easy to end up with your precision controlled by error in the arithmetic of the vertex transformation process. -
As mentioned earlier, Upchurch and Desbrun studied this and came up with two main recommendations to minimize roundoff error:
-
Use an infinite far plane.
-
Keep the projection matrix separate from other matrices, and apply it in a separate operation in the vertex shader, rather than composing it into the view matrix.
-
In many cases, separating the view and projection matrices (following Upchurch and Desbrun’s recommendation) does make some improvement. While it doesn't lower the overall error rate, it does seem to turn swaps into indistinguishables, which is a step in the right direction.
-
-
-
Upchurch and Desbrun came up with these recommendations through an analytical technique, based on treating roundoff errors as small random perturbations introduced at each arithmetic operation, and keeping track of them to first order through the transformation process.
-
float32 or int24 :
-
There is no difference between float and integer depth buffers in most setups. The arithmetic error swamps the quantization error. In part this is because float32 and int24 have almost the same-sized ulp in [0.5, 1] (because float32 has a 23-bit mantissa), so there actually is almost no additional quantization error over the vast majority of the depth range.
-
-
Infinite Perspective :
-
An infinite far plane makes only a miniscule difference in error rates. Upchurch and Desbrun predicted a 25% reduction in absolute numerical error, but it doesn't seem to translate into a reduced rate of comparison errors.
-
-
Reverse-Z :
-
The reversed-Z mapping is basically magic.
-
Reversed-Z with a float depth buffer gives a zero error rate in this test. Now, of course you can make it generate some errors if you keep tightening the spacing of the input depth values. Still, reversed-Z with float is ridiculously more accurate than any of the other options.
-
Reversed-Z with an integer depth buffer is as good as any of the other integer options.
-
Reversed-Z erases the distinctions between precomposed versus separate view/projection matrices, and finite versus infinite far planes. In other words, with reversed-Z you can compose your projection matrix with other matrices, and you can use whichever far plane you like, without affecting precision at all.
-
-
Conclusion :
-
In any perspective projection situation, just use a floating-point depth buffer with reversed-Z! And if you can't use a floating-point depth buffer, you should still use reversed-Z. It isn't a panacea for all precision woes, especially if you're building an open-world environment that contains extreme depth ranges. But it's a great start.
-
View Frustum
-
It's a region in Camera / View / Eye Space ; it's not a matrix or a separated space.
-
A view frustum is the truncated-pyramid volume (for perspective cameras) or box (for orthographic cameras) that defines the region of space potentially visible to the camera.
-
Objects outside it are clipped or culled.
-
Perspective View Volume :
-
The 3D region produced by a perspective camera: geometrically a truncated pyramid (frustum).
-
Points in view (camera/eye) space that lie inside this frustum are potentially visible and then mapped by the perspective projection matrix into the canonical volume (NDC).
-
This term is essentially the same concept as View Frustum for perspective cameras.
-
Parameters :
-
Field of view (or focal length), aspect ratio, near plane, far plane.
-
-
-
Orthographic View Volume :
-
A rectangular box (prism) defining the visible region for an orthographic (parallel) projection.
-
Unlike the perspective frustum, there is no perspective foreshortening; parallel lines remain parallel.
-
The orthographic view volume is mapped to the canonical view volume by the orthographic projection matrix.
-
Parameters :
-
Left, right, top, bottom, near, far.
-
-
-
Plane representation :
-
The frustum can be represented by six plane equations. Those are convenient for fast culling and intersection tests.
-
-
Frustum culling :
-
Is a performance test done usually on the CPU/GPU before or during rendering.
-
It tests bounding volumes (AABBs/spheres) against the six frustum planes (left/right/top/bottom/near/far) to skip drawing objects outside the frustum.
-
Those plane tests can be done in Camera / View / Eye Space (transform object bounds by the view matrix) or in World Space (transform the frustum planes into world space by the inverse view).
-
Orthographic Projection Matrix
-
A 4×4 matrix that implements an orthographic projection.
-
It uses linear (non-perspective) mapping in z and x/y and does not produce perspective foreshortening.
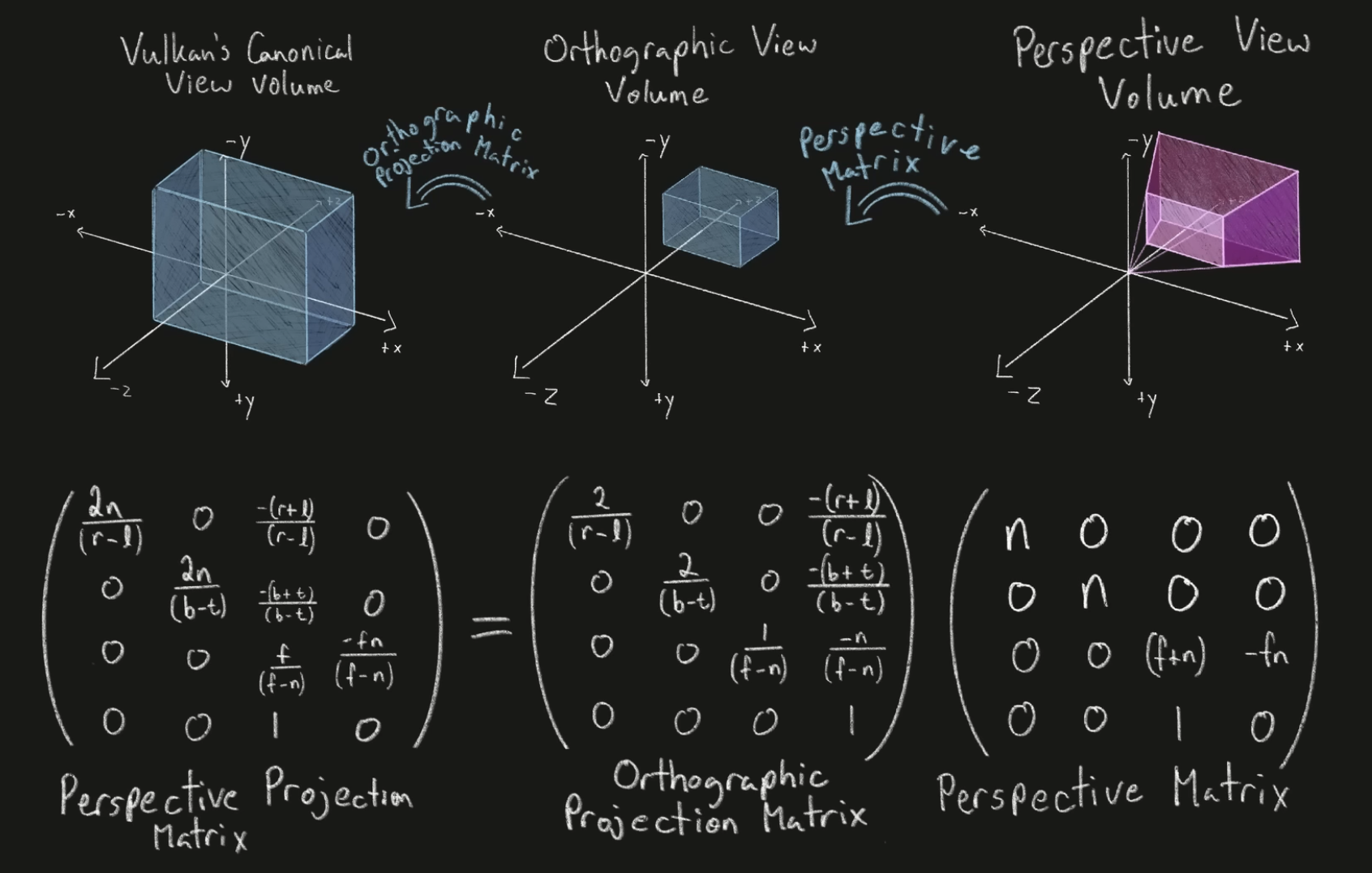
Perspective Projection Matrix
-
A 4×4 matrix that implements a perspective projection.
-
 .
.
-
 .
.
MVP Matrix / Model-View-Projection Matrix
-
The combined matrix (Projection × View × Model).
-
Multiply the model-space vertex by the MVP to get Clip Space homogeneous coordinates; it's not in NDC Space .
-
glm::mat4 MVPmatrix = projection * view * model; // Remember: inverted! -
Using a single combined matrix is common for efficiency.
Clip Space
-
4D Homogeneous space.
-
Clip Space Position :
-
It's the
gl_Positionin GLSL.
-
-
Projected Frustum / Canonical Clip Volume :
-
Exists in Clip Space after applying the Projection Matrix to the View Frustum .
-
The View Frustum is remapped so that:
-
Left, right, top, bottom planes align with
x=±w,y=±w. -
Near, far planes align with
z=±w(OpenGL) orz=[0,w](D3D/Vulkan).
-
-
It's the region the GPU will Clip against.
-
-
Clipping :
-
Is performed in clip space (or against clip planes).
-
Removes geometry outside the canonical clip volume (the projected Frustum).
-
This avoids producing fragments that should not be visible and prevents division-by-zero problems.
-
When to clip :
-
Reason it happens in clip space: the clip planes are linear in homogeneous coords; doing clipping after perspective divide would be non-linear and problematic.
-
Clipping in homogeneous clip space uses linear plane equations (easy and reliable).
-
If you divided first, you would get nonlinear boundaries and more complicated intersection math; also you could divide by 0 for points on the camera plane.
-
-
Perspective Divide
-
It's an operation to convert homogeneous clip coordinates to 3D (from Clip Space to Canonical View Volume / NDC / Normalized Device Coordinates ).
-
It's just an operation.
-
Divide
x,y,zbywfrom the Clip Space to get the Canonical View Volume / NDC / Normalized Device Coordinates . -
Once you perform the Perspective Divide , that Projected Frustum becomes the NDC Cube / Canonical View Volume .
NDC Space / Normalized Device Coordinates Space
-
3D non-homogeneous space.
-
Is the result derived from Clip Space by the Perspective Divide .
-
Geometry that lies inside the NDC Space will map into the Viewport .
-
NDC Cube / Canonical View Volume :
-
Obtained after performing the Perspective Divide in the Projected Frustum .
-
Is convenient because the next mapping to pixels is a simple affine transform.
-
-
Coordinates :
-
After a vertex is multiplied with this matrix X and Y, the resulting coordinates are position on the screen (between
[-1, 1]). -
The Z is used for the depth-buffer and identifies how far the vertex (or fragment) is from your camera's near plane.
-
-
Typical ranges :
-
OpenGL convention:
-
x ∈ [-1,1],y ∈ [-1,1],z ∈ [-1,1].
-
-
Direct3D / Vulkan convention:
-
x ∈ [-1,1],y ∈ [-1,1],z ∈ [0,1](Z-range differs).
-
-
Viewport Transform Matrix
-
Transforms NDC Space / Normalized Device Coordinates Space / Canonical View Volume to Window Coordinates / Screen Coordinates .
-
This transform is linear in X and Y but affine in Z, mapping NDC z-range to depth buffer range (
[0,1]or[-1,1]). -
This is the final transform before rasterization writes to the framebuffer.
-
The projection stage produces normalized coordinates that are independent of the actual render target size or position.
-
This transform gives those normalized coordinates a real position and scale on a particular render target (pixel grid + depth range).
-
Without viewport mapping, you would only have coordinates in
[-1,1]( NDC Space ); the rasterizer needs actual pixel locations (and a depth value in the depth-buffer range) to generate fragments and write pixels. -
The GPU/driver usually applies this mapping automatically (parameters set by API calls such as
glViewport/vkCmdSetViewport), but conceptually it is an affine transform applied after the Perspective Divide .
Screen Space / Screen Coordinates / Window Coordinates
-
2D coordinates in pixels (and a depth value).
-
It's the final stage before rasterization.
What Vulkan does implicitly
-
These are built-in, automatic steps the GPU will perform after your Vertex Shader runs, as part of the fixed-function pipeline:
-
Clipping :
-
Vulkan clips primitives against the Projected Frustum / Canonical Clip Volume automatically, based on the convention:
-
x,y ∈ [−w,w],z ∈ [0,w]in Clip Space .
-
-
This happens whether you use Perspective Projection or Orthographic Projection .
-
-
Perspective Divide :
-
Vulkan automatically divides
x,y,zbywfrom the Clip Space to get the NDC Space .
-
-
Viewport Transform Matrix :
-
Vulkan uses the
VkViewportparameters you provide to map NDC Space to Screen Space / Screen Coordinates / Window Coordinates . -
It also maps NDC Cube Z from
[0, 1]to your depth-buffer range (possibly reversed if you configure it that way).
-